Talk:Focal length
| This is the talk page for discussing improvements to the Focal length article. This is not a forum for general discussion of the article's subject. |
Article policies
|
| Find sources: Google (books · news · scholar · free images · WP refs) · FENS · JSTOR · TWL |
| This It is of interest to the following WikiProjects: | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
Diagram
[edit]I only started learning about focal length today, so if the diagram is wrong or can be improved let me know. - Redjar 01:36, 14 Oct 2004 (UTC)
herschel telescope of the 1700's
[edit]Has anybody any idea where I can find a picture of the early telescope by Herschel ?
send to malcolm.bennett@ntlworld.com thanks
EFL
[edit]In my own experience, the term "EFL" is used to express the equivalent size of a digital lens in 35mm terms. For example, on some Olympus cameras, since the size of the sensor is smaller, a 150mm lens will have the same angle of view as a 300mm lens would on a 35mm camera. That lens would be described as having an EFL of 300mm.
- I'm an amateur photographer and have been working in laboratory optics for the last four years and have never heard of this. EFL has a very well-defined meaning in terms of both traditional optics as well as consumer camera optics—it's the distance from the focal point to the first principle point. I strongly doubt an optically-saavy company like Olympus would deviate from the accepted standard on this...although I admit that I have been wrong in the past. --Milkmandan July 6, 2005 18:46 (UTC)
Convex & concave
[edit]I've re-generalized things a bit. It's important to note that convex and concave lenses are examples of converging and diverging lenses, not definitions of them. It's fine saying that in the picture caption, because the picture actually shows convex and concave lenses. But generally things are more complex. For example:
The third lens in this picture is a converging lens, but is both convex and concave. Therefore it's incorrect to define converging lenses as purely convex. --Bob Mellish 17:00, 25 October 2005 (UTC)
Too Technical
[edit]I find this article very heavy on the technical side, and it doesn't give an explaination in simple terms. Other photography terms have good basic descriptions, followed by more in-depth information.
- This is not a photography article. It is an optics article that happens to be of interest to photographers (at least those who want to know more about how their cameras work.)--Srleffler 00:40, 8 November 2006 (UTC)
- Agreed. It's great that we have the knitty-gritty of focal length here, but how about the simple description that it is, for practical purposes, quantified zoom? --User:RobertM525 00:26, 8 November 2006 (UTC)
- Part of the problem is that we have several communities intersecting in this article. Focal length is an extremely important concept in optics, and deserves a full explanation. If all photographers care about is that it is "quantified zoom", that's fine, but then there is little need for them to read this article.--Srleffler 00:40, 8 November 2006 (UTC)
- Perhaps some explicit disambiguation at the top of the article might help ? Something like :
- Photographers frequently quote a lens' focal length to quantify its angle of view; whilst the quantities are related, they are not equivalent. Also, the photographer's variable focusing distance (measured between subject and film plane) should not be confused with the focal length or focal distance of the lens. In geometrical optics, focal length specifies the optical power or magnification of a lens or curved mirror; by quantifying the distance from the mirror or lens to the point at which it focuses paraxial, parallel rays of light.
- ... and then go into the nitty gritty difference between mirror/lens' vertex vs. lens' principal plane, EFL, FFD, etc ? --Redbobblehat (talk) 14:49, 24 August 2009 (UTC)
- A historical side note : Lenses and curved mirrors were used since Antiquity as "burning glasses" (a kind of early "laser"); long before Kepler began to quantify their optical magnification properties. It is not difficult to imagine how a someone like Archimedes might measure the optimal distance from the burning glass to the tinder and give rise to a pre-optical, pragmatic concept of "focus distance", which c17th optics inherited and geometrical optics (Barrow / Newton [1]) diverged from. I would love to find a ref for this 'pre-optical concept', but the OED only gives the earliest known use of the optical terms "focal length" and "focal distance" to Halley's An Instance of the Excellence of the Modern Algebra, in the Resolution of the Problem of finding the Foci of Optick Glasses universally. (1673) [2] where he uses focal length / distance interchangeably to describe the BFD. --Redbobblehat (talk) 14:49, 24 August 2009 (UTC)
- You might find the roots of the term in mathematics. A focus of a conic section is a focal point of a mirror with that shape.--Srleffler (talk) 17:06, 24 August 2009 (UTC)
- Thanks Srleffer. My OED gives the latin "focus" as hearth or fireplace, and goes on to speculate that Kepler appropriated it to geometry in 1604 from it's "optical" sense as "the burning point of a lens or mirror (which is easily derived from the lit. sense) must have been already in existence" (OED 1979 "Focus"). However, I think that many of these geometrical-optical correspondences (Ray/Radius/Ra? is another one) quite probably go back to Euclid and/or Pythagoras (at least) - which is way beyond the scope of the OED! --Redbobblehat (talk) 19:23, 24 August 2009 (UTC)
- You might find the roots of the term in mathematics. A focus of a conic section is a focal point of a mirror with that shape.--Srleffler (talk) 17:06, 24 August 2009 (UTC)
Not only is the article very technical, but even this talk section is very technical. There really needs to be a SIMPLE explanation of what focal length is at the top of the article, rather than diving straight in to its characteristics. As it stands, it is like describing a human being solely in terms of its thermodynamic properties. What is needed, for example in the case of photography, if the focal length is the distance between the lens and the object being photographed, why not just say that? If it is something else, eg that goes in inside a optical instrument, perhaps a diagram that is annotated in technical terms would work. As it stands, from reading this article, I still don't know what focal length is. FreeFlow99 (talk) 16:02, 30 April 2021 (UTC)
- ...because that wouldn't be true. The focal length is not the distance between the lens and the object being photographed. It is also not, in general, the distance from the lens to the ccd sensor or film. In a very simple optical system—a very thin lens, focusing light from a distant object—the focal length is the distance from the lens at which the image of the object forms. This is shown in the first image in the article. Once you get into more complicated optical systems, the focal length becomes an abstract thing; it's not a distance from any one thing to any other thing, it's just a measure of how "strong" the lens is.
- Opticians do this the right way. They don't work with focal length at all, but instead use one over the focal length, which is called the optical power. You'll see this on eyeglass prescriptions: the numbers are written in Dioptres; units of optical power. Optical power is a real and intuitive measure of a lens; focal length is not in general.--Srleffler (talk) 21:42, 2 May 2021 (UTC)
millimeters?
[edit]Where would I find information about camera focal length measured in millimeters? I followed some links from this page but didn't find the right page. I'd think this page should link to wherever that answer is. —Ben FrantzDale 22:30, 26 February 2007 (UTC)
- I'm not sure what information you are looking for. Did you try Photographic lens?--Srleffler 23:51, 26 February 2007 (UTC)
- That's enough to get me started. Thanks. I'll ad a DAB at the top of this page. —Ben FrantzDale 21:19, 27 February 2007 (UTC)
Disambiguation
[edit]The concept of "focal length" is also used in relation to pinhole cameras to describe the distance between the camera pinhole and the image plane. To me this is a not really the same this as the focal length described in this article which is more related to convergence of lenses and optical systems in general. Even though a pinhole camera is a type of optical system, I still don't see these two focal length concepts as the same thing. In any case I want to be able to make a short description of "focal length" in relation to the pinhole camera somewhere so that it is possible to use a simple wikilink to find it. Possible alternatives:
- It can be done in a separate section in this article + adding the alternative defintion in the lead section.
- Turn this article into a disambiguation page which links to "Focal length (optical systems)" which will host this article and "Focal length (pinhole camera)" which takes care of the pinhole case. Maybe "optical system" is not a good qualifier since a pinhole camera is an optical system as well? Perhaps "lens systems" is better?
Any opinions?
--KYN 08:43, 7 August 2007 (UTC)
Fixed using a {{this article is about}} template. --KYN 15:10, 17 August 2007 (UTC)
Definition
[edit]In photography, the focal length of a lens is defined as as the distance from the optical center of a lens (or, the secondary principal point for a complex lens like a camera lens) to the focal point (sensor) when the lens is focused on an object at infinity.
In the pinhole camera model the focal length is the distance between the pinhole (optical centre) and the image plane.
I think these definitios should be somehow inlcuded in this article. —Preceding unsigned comment added by 217.154.24.242 (talk) 16:56, 4 September 2007 (UTC)
- The definition in photography is the same as the one used in physics. This article is more general in scope, and has to be more careful about how things are defined.
- From the article:
For a thin lens in air, the focal length is the distance from the center of the lens to the principal foci (or focal points) of the lens. For a converging lens ... the focal length is positive, and is the distance at which a beam of collimated light will be focused to a single spot.
- and
For an optical system in air, the effective focal length gives the distance from the front and rear principal planes to the corresponding focal points.
- I'll try to add a more contextual description to the section on photography.--Srleffler 03:03, 5 September 2007 (UTC)
- By the way, photographers should probably drop the phrasing that the focal length is the distance from the "optical center" of the lens to the focal plane. It is misleading, particularly for camera lenses. The focal length is always the distance from a principal plane to the corresponding focal plane. The principal planes can generally only be taken to be at the center of the lens when the lens is much thinner than the focal length, which is almost never the case for camera lenses. In (almost) every other case there are two principal planes and it is misleading to refer to either of them as the lens' "optical center".--Srleffler 03:14, 5 September 2007 (UTC)
- The article intro was missing a basic definition. I adapted one from Wiktionary[3] and Focus (optics). It all may need rewording and checking against some source since references are non-existent at those articles. I also reworded the description that seemed to imply that this just applies to photography, it actually applies to many optical systems. MrFloatingIP (talk) 15:48, 12 September 2009 (UTC)
- Dropping this in here since there seems to be a conflict:
- In optical systems, focal length is the distance between a lens or mirror and its focus or focal point, as measured from a lens or mirror's principal point or principal plane along the optical axis. Focal length is a measure of how strongly an optical system converges (focuses) or diverges (defocuses) light. A system with a shorter focal length has greater optical power than one with a long focal length; that is, it bends the pencil of rays more strongly, bringing them to a focus in a shorter distance. Longer focal length, or lower optical power, is associated with a larger image magnification of distant objects, or a narrower angle of view. Conversely a shorter focal length, or higher optical power, is associated with a wider angle of view.
- MrFloatingIP (talk) 16:31, 12 September 2009 (UTC)
- As to reverts, the article does not currently conform with WP:V since it does not include the basic definition in almost every reference[4], or WP:LEAD re- "If its subject is amenable to definition, then the first sentence should give a concise definition: where possible, one that puts the article in context for the nonspecialist" and MOS:BEGIN "text needs to unambiguously define the topic for the reader, without being overly specific". Because of this I am dropping a version with the definition in as a starting point. MrFloatingIP (talk) 17:09, 12 September 2009 (UTC)
- Focal length isn't so easy to define exactly. In the most general case (e.g. a thick lens with different media on each side, neither of which has n=1), the focal length is not a distance from anything to anything. The quantity with real physical significance is the optical power. It's easier to define in the limited case of an optical system where the object and image spaces have n=1. I added a statement for that case to the intro. The wording can probably be improved.--Srleffler (talk) 17:22, 12 September 2009 (UTC)
- The definition you put in the article is not sufficiently general. It isn't true for an optical system where the surrounding medium is not air or vacuum, for example. In that case the focal length is not the distance from a principal plane to a focus. That distance is the focal length times the index of refraction. --Srleffler (talk) 17:02, 12 September 2009 (UTC)
- That may be true but we still need to meet WP:V (re: all the definitions out there) and MOS:BEGIN "overly specific". Looks like some more rewording could be done. MrFloatingIP (talk) 17:30, 12 September 2009 (UTC)
- I think that defining the topic is not exactly the same as precisely defining "focal length". We need to do both; the technical definition probably shouldn't be in the first sentence, but should be in the lead. Dicklyon (talk) 17:35, 12 September 2009 (UTC)
- Regarding WP:V and the google search you linked to above: note that in the context of WP:V only reliable sources are relevant. We need not pay attention to definitions given in non-reliable sources. In fact, most of the definitions of focal length one sees online are incorrect.--Srleffler (talk) 18:43, 12 September 2009 (UTC)
what we are seeing right now would not be possible without the focal length. — Preceding unsigned comment added by 114.79.152.116 (talk) 03:09, 12 February 2012 (UTC)
Unclear sentence in the Photography section
[edit]| “ | When the lens is adjusted to photograph objects closer to the camera, the actual focal length of the lens changes. | ” |
This sentence seems incorrect to me. When the lens is adjusted to photograph objects at a less-than-infinite distance, the focal length of the lens doesn't change... it's just that the lens moves further from the image plane (film or sensor), so that the rays from the object converge in points on the appropriate surface.
As in this diagram from the lens article:

If , then , so the lens must be moved further from the image plane.
Maybe some photographic lens designs employ a complex construction that doesn't require moving the lens further from the image plane, but all of the ones I own seem to obey this principle.
Should this sentence be changed? I'm trying to think of a clear way to explain how the camera lens moves in order to focus objects at different distances. Any suggestions? ǝɹʎℲxoɯ (contrib) 03:50, 17 January 2008 (UTC)
- I think you're right. I wrote that sentence, and I'm not sure what I was thinking.--Srleffler (talk) 04:17, 17 January 2008 (UTC)
- I changed it. It's likely that for some lenses it was true, but I don't think that's what he was trying to say. I'm not sure about principal planes, but I'm pretty sure that what I said about the rear nodal point is true, and it agrees with the diagram on that page. Dicklyon (talk) 04:13, 17 January 2008 (UTC)

F, F' front and rear focal points,
P, P' front and rear principal points,
V, V' front and rear surface vertices.
- I'm certain principal plane is correct for a lens in air. I can't recall if the nodal points coincide with the principal planes in that case. Which diagram are you referring to?--Srleffler (talk) 04:25, 17 January 2008 (UTC)
- Yeah, I'm not sure which is more correct and standard here... principal point or nodal point? In air, they're at the same place. ǝɹʎℲxoɯ (contrib) 04:36, 17 January 2008 (UTC)
- Thanks! I expanded on your changes by adding an example to show how a 50 mm lens must move about 2.6 mm to go from infinity to close focus, hopefully this will be a useful real-world example. ǝɹʎℲxoɯ (contrib) 04:36, 17 January 2008 (UTC)
- Note that when the lens is focused on objects not at infinity, the rear focal plane no longer coincides with the image plane. The focal planes are explicitly the planes containing the focal points—they are separated from the principal planes by f. Also note that the equation
- in your example is not actually the thin lens equation. It has the same form, but you are interpreting the variables differently. In the thin lens equation S1 and S2 are measured from the center of the lens. Camera lenses aren't "thin", so the locations of the principal planes have to be taken into account.--Srleffler (talk) 04:58, 17 January 2008 (UTC)
- Note that when the lens is focused on objects not at infinity, the rear focal plane no longer coincides with the image plane. The focal planes are explicitly the planes containing the focal points—they are separated from the principal planes by f. Also note that the equation
- Thanks! I expanded on your changes by adding an example to show how a 50 mm lens must move about 2.6 mm to go from infinity to close focus, hopefully this will be a useful real-world example. ǝɹʎℲxoɯ (contrib) 04:36, 17 January 2008 (UTC)
- Yeah, the optical term focal plane doesn't quite agree with what photographers call the focal plane, which is their film is, which is really the image plane. Should we mention the different interpretation of the term? Dicklyon (talk) 05:59, 17 January 2008 (UTC)
- Probably a good idea.--Srleffler (talk) 06:29, 17 January 2008 (UTC)
- Yeah, the optical term focal plane doesn't quite agree with what photographers call the focal plane, which is their film is, which is really the image plane. Should we mention the different interpretation of the term? Dicklyon (talk) 05:59, 17 January 2008 (UTC)
- Good point. Is there a name for the equation when used with non-thin lenses? ǝɹʎℲxoɯ (contrib) 07:35, 17 January 2008 (UTC)
- I was looking for a technical description of focal length as it applies to photography and didn't find it here. The most odd thing for a newbie is that focal length in photography has little to do with focus. I think there should be a page dedicated to that, say focal length (photography), since it is used to describe view angle, among other things. There is some information on photographic lens, but it doesn't go into detail. For example, is the focal length of a lens a real thing you can measure (e.g., the distance from the exit pupil to the image plane) or is it really used as a surrogate measure to describe view angle. For example, I think you can have a wide-angle lens that is image-space telecentric. I'll be bold and start that page. —Ben FrantzDale (talk) 01:33, 18 January 2008 (UTC)
- What do you mean by "focal length in photography has little to do with focus"? It has everything to do with focus; also with magnification. It determines where to put the film to get an image in focus, and it determines what the subject magnification will be (mapping of distant object angle to image size, or object size to image size if you know object distance). See pinhole camera model. Dicklyon (talk) 05:24, 18 January 2008 (UTC)
- Focal length is a real measureable thing, but doesn't have to do with exit pupil, nor does it determine the field of view (even when combined with format size, you still need to know the distortion to get an accurate angle of view). Yes, you can have a short focal length lens that's telecentric on the image side, since distance to exit pupil is unrelated to focal length; focal length is distance to rear nodal point. Simple definition: it's the distance from image plane to a pinhole that would image a distant small object the same size as the lens in question. Dicklyon (talk) 02:40, 18 January 2008 (UTC)
- I just checked out your new focal length (photography), and converted it to a redirect to focal length. Use the Template:Split-apart or Template:Splitsection tag (in double curly braces) on this article if you'd like to propose a content split. I'll probably oppose it. Dicklyon (talk) 02:53, 18 January 2008 (UTC)
- Ben, are you perhaps confusing focal length with focus distance? The former (the subject of this article) is a property of the lens, while the latter is the distance to the object that you want to focus on. Those two are then of course related to the distance to the image plane, by the lens equation. I think it might be common to mix them up... ǝɹʎℲxoɯ (contrib) 08:48, 18 January 2008 (UTC)
- I'm not confused now, but I used to be. To someone new to the subject (i.e., someone who just got an SLR), it seemed baffling that people would talk of "focal length" when it seemed more natural to think of angle of view. While it does have something to do with focus, once you have a camera in hand, you can focus at almost any distance without changing the focal length, so for someone coming at this from a photography perspective, calling it "focal length" seems unnatural. That's why I wanted to see a page dedicated to the photographic use of the term.
- I think the first paragraph of the photographic description of focal length should say something like "The focal length of a camera lens describes the distance from the film plane to the pinhole of a pinhole camera that would produce images with the same projection." To many, that (phrased better) would be sufficient. But personally, I am still having trouble seeing how the "focal length" of a lens system necessarily corresponds to the projection you see on the sensor. (Thanks for all your patience in helping me understand this. Once I understand it, I'll see to it that the article is clear to the next person who comes upon it from my perspective.) —Ben FrantzDale (talk) 15:26, 19 January 2008 (UTC)
- Ben, I agree that it *is* more intuitive for photographers to think of focal length in terms of angle of view. However it is also quite intimately related to the distance between the lens and the image plane. I have recently improved (hopefully) the angle of view article to include a diagram that explains the relationship between distance to the image plane, focal length, and angle of view:
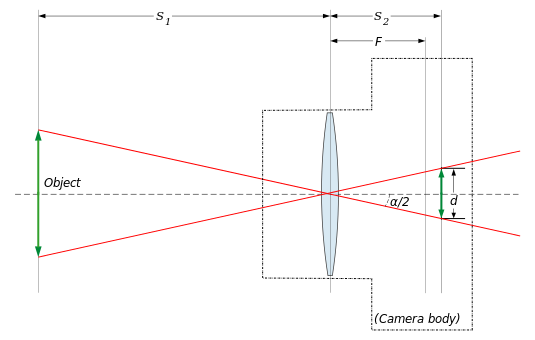
- What do you think of the accompanying text? Does it clarify the situation somewhat?
- Perhaps there is a good way to integrate the information there into this focal length article, or link to it appropriately... ǝɹʎℲxoɯ (contrib) 23:07, 19 January 2008 (UTC)
- I'm thinking that the symbols and names used in that article may lead to confusion. In optics, the focal length is conventionally represented by a lower case f. The upper-case F is the symbol for the focal point itself. Additionally, "focal length" and "effective focal length" are the same thing. (There are other focal lengths in an optical system, such as the front focal length and the back focal length, which differ from the e.f.l.) The angle of view article defines effective focal length f, but then distinguishes from the stated focal length of the lens F. The text implies that the focal length changes, in particular that f and F differ for macro photography, where
- .
- I haven't tried to analyze it, but this looks wrong. At the least, unless the focal length of the camera lens actually changes, the article is using "effective focal length" in a way that disagrees with standard optics usage. Perhaps this is again just confusion over the fact that the film is not always at the focal plane of the lens?--Srleffler (talk) 00:40, 20 January 2008 (UTC)
- Depends on what you mean by "wrong". The term "effective focal length" is sometimes used to mean the focal length adjusted for lens extension for close focusing, which narrows the angle of view. I think the formula is right, at least in the thin-lens or pinhole approximation. The terminology may be "wrong", however; do you have a better term for this distance? Dicklyon (talk) 00:56, 20 January 2008 (UTC)
- Yes, that's the case here, "effective focal length" means "distance to image plane adjusted for close focusing." That terminology was in the article before I edited it. It should just be called "image plane distance", but since photographers are accustomed to that being roughly equal to focal length, that might lead to confusion. ǝɹʎℲxoɯ (contrib) 01:30, 20 January 2008 (UTC)
- The terminology has been in angle of view since 2003, this diff. I would have written it the same way; there's also the "effective f-number" concept for f-number adjusted by lens extension (same 1+m factor, but in the denominator). Dicklyon (talk) 01:49, 20 January 2008 (UTC)
- Yes, that's the case here, "effective focal length" means "distance to image plane adjusted for close focusing." That terminology was in the article before I edited it. It should just be called "image plane distance", but since photographers are accustomed to that being roughly equal to focal length, that might lead to confusion. ǝɹʎℲxoɯ (contrib) 01:30, 20 January 2008 (UTC)
- Depends on what you mean by "wrong". The term "effective focal length" is sometimes used to mean the focal length adjusted for lens extension for close focusing, which narrows the angle of view. I think the formula is right, at least in the thin-lens or pinhole approximation. The terminology may be "wrong", however; do you have a better term for this distance? Dicklyon (talk) 00:56, 20 January 2008 (UTC)
- I'm thinking that the symbols and names used in that article may lead to confusion. In optics, the focal length is conventionally represented by a lower case f. The upper-case F is the symbol for the focal point itself. Additionally, "focal length" and "effective focal length" are the same thing. (There are other focal lengths in an optical system, such as the front focal length and the back focal length, which differ from the e.f.l.) The angle of view article defines effective focal length f, but then distinguishes from the stated focal length of the lens F. The text implies that the focal length changes, in particular that f and F differ for macro photography, where
I want to follow up on this. I still don't buy it. It now says:
- When a photographic lens is focused at "infinity" (e.g., at a distant mountain), its rear nodal point is separated from the sensor or film, at the focal plane, by the lens's focal length.
I still have trouble believing this. If I had two lenses with the same listed focal length but different angles of view on the same sensor, I would be justifiably upset, no?
Obviously if we have a camera lens with just one thin element at the aperture, it will have "well-behaved" focal length in that the angle-of-view definition would agree with the nodal-point definition. Suppose we halve the focal length of the lens element, make it bigger, and move it half way between the aperture and the sensor (so we will still be focused at infinity). Did the focal length halve? By the present definition, it must. But the sketches I'm drawing (I don't have ZEMAX in front of me) suggest that the angle of view won't change that much.
With that in mind, it seems like one of these must be true:
- Focal length in photography is really just "focal length of image-equivalent pinhole camera"
- Focal length in photography does not actually determine the angle of view on a given sensor format.
Which is it? —Ben FrantzDale (talk) 14:26, 8 November 2010 (UTC)
- Ben, you should work out stuff like this in a discussion forum, or work it out yourself from Zemax or other tools, because it's quite a distraction for wikipedia editors to have to try to talk you through your confusion. The article is correct. Focal length and rear nodal point are well defined as described in the article. The field of view for a given focal length can vary a bit, between rectilinear and fisheye lenses for example; focal length determines the magnification of distance objects in the center of the image, that is, size per subtended angel when focused at infinity, as if there were a pinhole at the rear nodal point. Dicklyon (talk) 16:17, 8 November 2010 (UTC)
- Dicklyon, I apologize if this comes across as a distraction; there are a lot of ways to think about these things, and while sometimes many can agree, sometimes that isn't the case. The article left me confused, and I know more than most photographers about this stuff, so I assume my naivety applies to many readers and so isn't distraction. I found an answer to my question, I think: This wide-angle-lens review shows an example of a 15 mm Canon fisheye with a wider angle of view than a low-distortion 14 mm Canon lens. That tells me that focal length in photography really is the paraxial focal length and so doesn't fully define the angle of view on a given sensor format. That said, I think it is safe to say that for practical purposes a photographer can use pinhole-lens geometry to estimate the angle of view of a given lens, there just may be caveats for ultra-wide or otherwise distorted or unusual lenses. I find this surprising and quite an interesting result. —Ben FrantzDale (talk) 18:56, 15 November 2010 (UTC)
- After playing with ZEMAX and finding the review linked above, I think I understand. The focal length listed describes only the center of the image (as illustrated by the review). In the case that the entrance pupil coincides with the front nodal point, the exit pupil will necessarily coincide with the rear nodal point, and so the image geometry corresponds to the pinhole approximation.
- If you contrive a lens with the entrance pupil in a different place along the optical axis, then an object point some sufficiently small angle from the optical axis will still be able to see the front nodal point, so that ray will land in the correct place on the sensor (WRT the pinhole model). The rest of the pencil from that object point to the entrance pupil will land in the same spot—failure to do so can be chalked up as an optical aberration (I think).
- The interesting case that I was hung up on (but that is ultimately irrelevant to the definition) is if you have a small entrance pupil sufficiently far from the front nodal point that there are object points that can't see it. Those object points will necessarily be imaged in the "wrong" place (WRT the pinhole model) and so those areas will be distorted. This case is irrelevant, though, because we can always move toward the optical axis to find an object point that sees the front nodal point as arbitrarily close to the center of the entrance pupil, and it is only this central image patch with which focal length in photography is concerned.
- That explanation explains all of my concerns. It's that the entrance pupil diameter must be finite and this only describes the image center. Thanks for all your help. —Ben FrantzDale (talk) 16:21, 16 November 2010 (UTC)
Wrong sign convention for formulas
[edit]There is either an error in the formulas here or the sign convention is described wrong. The formula for the effective focal length is clearly wrong given the sign convention described for the radii of curvature. It's correct for the sign convention described at Radius of curvature (optics), and that used at Lens (optics), however. Assuming I'm not making a mistake, I think we should fix the description of the convention used rather than changing the formulas.--Srleffler (talk) 05:44, 24 February 2008 (UTC)
Normal Lens Myth
[edit]| “ |
|
” |
This whole paragraph is so wrong. Hasn't got anyone a standard/normal lens anymore? Please, mount one on your camera and take a look -- the ANGLE-OF-VIEW is much smaller than that of the human eyes. The apparent PERSPECTIVE of a standard lens is similar to the human perception apparatus, i.e., the things seem to have the same spacial relations to one another in a picture taken with a standard lens as when we view them in real life. For wide angle lenses, these relations seem exaggerated (close things seem closer than they really are, and farther things look farther), whereas teles show a flattened perspective where things look closer together.
Our two eyes have a angle-of-view of about 180°, so a 16mm lens or so is needed to render the same field-of-view. But the human perception apparatus is very different from an optical lens. We have only a narrow "center of attention" which probably equals a 200mm or 300mm lens. For example, when reading, we see the complete page in our field-of-view, but still need to "move" from word to word instead of just perceiving the whole text in our vision. It's all a quite complicated matter, but the myth that a standard lens is anywhere close to equivalent to our angle-of-view needs to be eradicated. —Preceding unsigned comment added by 145.253.2.232 (talk) 01:54, 5 April 2008 (UTC)
- I suspect that our sense of "normal" has a lot to do with how we like to look at pictures. My suspicion is that a picture taken with a "normal" lens viewed at a usual distance for that medium will produce the approximately the same image on your retina as if your pupils were at the same location as the camera's was. With 135 film and a normal lens, you have an angle of view in the long direction of 40° (2*atan((36mm/2)/50mm)). That's the same angle as the long direction of a 4"x6" print held at 8.3". If you printed the same picture on paper 10" wide and held it 13.9 inches from your eye, you would have the same image on your retina. If you took the same picture but with a 25mm lens, the middle half of the image would be identical to the image taken with the 50mm lens. If you printed it at 8"x12" and held it 8.3" from your eyes, you would again have the same image on the middle of your retina, but you would have a wider field of view.
- I haven't seen citations to support my argument, but in general, perception of "normal" must depend on viewing conditions. I imagine the most "normal" seeming picture would be taking a picture with a 180° angle of view and printing it on the inside of a hemisphere. —Ben FrantzDale (talk) 17:36, 5 April 2008 (UTC)
- The myth has been so often repeated that some people accept it in spite of its contradiction. But the subject is discussed more sensibly, sort of like what Ben is talking about, here. Dicklyon (talk) 18:08, 5 April 2008 (UTC)
- I fixed the article per that source. Dicklyon (talk) 18:32, 5 April 2008 (UTC)
- Dicklyon, thanks for the reference. We should be sure that normal lens includes that information as well. —Ben FrantzDale (talk) 03:13, 6 April 2008 (UTC)
What has more zoom?
[edit]The article says that a system with a shorter focal length has greater optical power than one with a long focal length. Then why does a a 300 mm lens have more magnification than a 70 mm lens? --The High Fin Sperm Whale (talk) 04:23, 21 May 2009 (UTC)
- Good question. I'll answer it on the page, but the quick version is that the focal length describes the way the image is projected onto the film/sensor as though the camera is a pinhole camera. Since a camera is not a pinhole camera but has an aperture, the lens is needed to focus the rays. In order to bring the exit pupil closer to the sensor/film, you need more optical power (ability to bend light) in order to focus the rays. —Ben FrantzDale (talk) 12:30, 21 May 2009 (UTC)
- Basically, I'd say that the everyday notions of "power" and "magnification" don't match up intuitively with respect to optics. "Optical power" is the ability of a lens to bend light, while "magnification" represents the relative size of an object and its image. Turns out that these often are inversely correlated in building a practical camera! Moxfyre (ǝɹʎℲxoɯ | contrib) 15:37, 21 May 2009 (UTC)
- One more thing: For general-purpose photographic lenses that can focus at infinity, what I said above holds. That is not true for macro lenses and microscopes because "focal length" as it is used in photography generally assumes you want to focus at infinity. If you want to form an image of something with one element (e.g., a magnifying glass) where you want the image to be 100mm behind the lens, you might think you'd want a lens with a focal length of 100mm. You do if you want to focus at infinity, but now suppose you want to focus at 50mm in front of the lens (assume for the sake of simplicity you have a magically zero-thickness lens). Now you need a much more powerful lens because you need to bend the rays much more. In the extreme case of microscopy (in which you talk about numerical aperture rather than f/number), you have a subject that is very close to the entrance pupil, so the cone of light leaving a point on the sample entering the pupil may be very wide. There are more details, to be sure, but if you look at a high-power microscope objective you can see a series of very powerful (in the optics sense) lenses trying very hard to bend a lot of light.
- Another limitation with both microscopes and telephoto lenses is aperture size and the diffraction limit. While simple geometric optics says that a long-focal-length lens should require less-powerful optics, you do still need to (a) capture enough light to make an image and (b) have a big enough aperture to stay away from the diffraction limit. While these constraints may not require powerful lenses in the optics sense, they do require very good lenses. For example, the Canon EF 1200mm f/5.6 lens has a 21.4 cm entrance pupil! That's over eight inches! That means many of the elements are that big across and high-quality across that huge area, so even if they aren't powerful, it's not a surprise that it's almost a $90,000 lens. See also Magnification. —Ben FrantzDale (talk) 20:10, 12 June 2009 (UTC)
difference between 'focal length' and 'focal distance'
[edit]Stewart's Optical Principles and Technology for Engineers highlights a crucial (and logical) difference between front focal length (FFL) and front focal distance (FFD):
- p.34 : " The focal length of a lens is measured from the focal point to the corresponding principal point, not to the surface of the lens. The focal distances measured from the lens surfaces are the back focal distance and the front focal distance."[5]
- p.63 : "The distance from the first focal point to the first principal plane of the combination is the front focal length, fFF." [6]
which is supported in Grievenkamp's Field Guide to Geometrical Optics p.6
- "The front and rear focal lengths (...) are defined as the directed distances from the front and rear principal planes to the respective focal points" "[7]
Using this terminology, a lens' EFL = BFL = FFL only when the object and image space media have the same refractive index - "in air" - which is by far the most common case. However, when the refractive index of the media in front (object-side) and behind (image-side) of the lens are different: the effective FFL ≠ BFL, so the distinction is an important one.
Whilst no-one would ever dream of saying "focal length = focal distance", some authors ([8], [9]) are still quite content to use "FFL = FFD" and (are forced to) use "first focal length" and "second focal length" when front and back media have different refractive indices. Not only is this logically messy, but I can see this numbering system causing problems with a multiple-lens system: it would seem helpful to be able to compare the "first back focal length" with the "second front focal length", etc ...
In "common" usage, then, it seems that "front focal distance" and "first focal length" are safely unambiguous, but "front focal length" could be used to refer to either of them.
- Menzel, Fundamental Formulas of Physics, vol.2 p.384 : "The quantity f is called the equivalent focal length of the system in object space, or the first focal length, and often the front focal length. Similarly the quantity f' is called the equivalent focal length of the system in image space, or the second focal length, and often the back focal length. (It should be noted that the terms front and back focal length are often used at the present time to describe the distance from the first focal point to the front vertex of the lens, and from the rear lens vertex to the second focal point. This confusion is not desirable, and the terms front and back focal distances are recommended instead. The terms front focus and back focus are also used.) Where initial and final media have identical indices, it is clear from the above formula that the two focal lengths are equal." [10]
--Redbobblehat (talk) 14:30, 23 August 2009 (UTC)
- Yes. It's hard to treat this well though because usage varies between different authors. I believe at one time this article used Greivenkamp's definitions, but the text was adjusted because some authors do use FFL for the vertex-to-focus distance. The text does correctly describe how some authors distinguish between FFL and FFD. While textbooks lean toward the "FFL=principal plane to focus" usage, vendor catalogs and the like tend to use FFL/BFL for vertex to focus distance. --Srleffler (talk) 00:47, 24 August 2009 (UTC)
- Perhaps, following Menzel's treatment, we should relegate front focal length and back focal length to an explanatory (disambiguation) section, and the rest of the article should encourage - for wikipedia purposes - the unambiguous use of front focal distance, back focal distance, second focal length and first focal length? ... IMO this wrankles :( but for the sake of wikipedians with different 'background reading' it's the best practical compromise I can think of. --Redbobblehat (talk) 11:36, 24 August 2009 (UTC)
- It rankles me too, mainly because "first focal length" etc. is (I think) a much less commonly used term. I'm not sure I have ever seen it before. --Srleffler (talk) 17:00, 24 August 2009 (UTC)
- Perhaps, following Menzel's treatment, we should relegate front focal length and back focal length to an explanatory (disambiguation) section, and the rest of the article should encourage - for wikipedia purposes - the unambiguous use of front focal distance, back focal distance, second focal length and first focal length? ... IMO this wrankles :( but for the sake of wikipedians with different 'background reading' it's the best practical compromise I can think of. --Redbobblehat (talk) 11:36, 24 August 2009 (UTC)
- A side point: note that in Greivenkamp's formalism in the most general case, the focal length (or EFL) is not the distance from a principal plane to a focus. I have often thought that it would be more sensible to abandon the effective focal length altogether, and use optical power instead. For real, general lens systems, it is not really a measure of physical length, but rather a measure of how strongly the lens converges light. It's only in the simple case of a thin lens in air that it becomes so intuitive to think of "focal length".--Srleffler (talk) 00:47, 24 August 2009 (UTC)
in photography
[edit]When I read in this section "When a photographic lens is set to "infinity", its rear nodal point is separated from the sensor or film, at the focal plane, by the lens's focal length." I thought 'oh no here we go again ...'. But when I looked at Joseph Wisniewski's magnum opus "Lens Table 1" I was very pleasantly surprised! Unfortunately I suspect this reference doesn't meet wikipedia standards, but it may be helpful in debate.
Another statement in this section is much more problematic : "The focal length of a lens determines the magnification at which it images distant objects. The focal length of a lens is equal to the distance between the image plane and a pinhole (see pinhole camera model) that images distant small objects the same size as the lens in question. Combining this definition with an assumption of rectilinear imaging (that is, with no image distortion) leads to a simple geometric model the photographers use for computing the angle of view of a camera." IMO this article should not even mention this tricky topic, which revolves around whether or not the focal length is a good approximation of ... some other variable! It should be confined to Angle_of_view#Derivation_of_the_angle-of-view_formula. —Preceding unsigned comment added by 83.100.130.143 (talk) 03:09, 4 February 2011 (UTC)
- It wasn't very clear and it wasn't sourced, so Srleffler took it out. I rewrote it, hopefully better, with sources, because I didn't want to leave a simple statement that wasn't true and didn't really say what focal length is. In general, the ratio of focal length to film or sensor size is not quite enough to calculate an angle of view; it works for the special case of rectilinear imaging, that is, when the lens acts like a pinhole; but not when it has distortion, as in the extreme case of a fisheye lens. Dicklyon (talk) 06:23, 4 February 2011 (UTC)
- Photographers' Formulae for angle of view, depth of field and focusing distances may make use of focal length, but they should not be treated in this article. Almost all of this article's "in photography" section belongs in angle of view, not here. I agree with Srleffler - it should be removed entirely from this article. Perhaps a new article "focusing (photography)" would also be a useful place to off-load the rest ? If not, a small concession would be to retain here something like :
- The focal length of a photographic lens indicates the distance between the lens' rear nodal point and focal plane. The lens' focal plane coincides with the camera's film plane only when the lens is focused at infinity. Closer focusing is achieved by increasing the distance between the focal plane and the film plane. Increasing this gap (the "focusing extension"[11]) allows nearer objects to be brought into focus on the film. Focal length should not be confused with focusing distance, which is measured from the film plane to the in-focus object. In photography, focal length is often used in calculating depth of field. It is also common for photographers to use a lens' focal length to calibrate its approximate angle of view and magnification. Both focal length and dioptres measure optical power and so are easily interchangeable.
- Section "3. Image-side perspective point" of John Bercovitz 1998, Image-side Perspective and Stereoscopy, (SPIE proceedings vol. 3295) presents an analysis of the geometrical relationships between a lens' pupils and cardinal points. If anyone can understand it enough to re-present it in a more easily accessible form, then I for one would be very grateful! However, I'm not sure which article should best summarise Bercowitz' exegesis - neither focal length, angle of view, nor cardinal points seems quite right.
- --Redbobblehat (talk) 23:41, 4 February 2011 (UTC)
- Photographers' Formulae for angle of view, depth of field and focusing distances may make use of focal length, but they should not be treated in this article. Almost all of this article's "in photography" section belongs in angle of view, not here. I agree with Srleffler - it should be removed entirely from this article. Perhaps a new article "focusing (photography)" would also be a useful place to off-load the rest ? If not, a small concession would be to retain here something like :
- That stuff belongs in cardinal point.
- I agree that the "in photography" section is not great, and too long, but I do think that the relationship of FL to angle of view is the main thing that people interested in photography will want to know about. Perhaps a brief statement and a main link would be a better way to do it? Dicklyon (talk) 04:47, 5 February 2011 (UTC)
- Yes, yes and yes. Slingshot them to AOV :-) --Redbobblehat (talk) 05:56, 5 February 2011 (UTC)
- Dick, a good start! but it might be easier and quicker to simply start afresh rather than chip away at the existing text? I've re-edited my 'draft' paragraph above ("The focal length of a photographic lens indicates ... "). Would this be a useful starting point for the 'in photography' section ? IMO it is still too long : The lens-focus mechanism bit seems to wander off topic, but AFAIK it's not explained elsewhere on wikipedia ? Can you think of any other 'legitimate' uses of focal length in addition to DOF ? The bit about dioptres is not specific to photography, but might go elsewhere in the article? Are any of the statements unclear or inaccurate ? --Redbobblehat (talk) 15:01, 6 February 2011 (UTC)
- The formal definition "indicates the distance between the lens' rear nodal point and focal plane" doesn't really tell you anything useful unless you already understand nodel points. The explanation in terms of magnification and equivalent pinhole, on the other hand, stands alone. Why would you want to obscure the meaning by putting it in terms of concepts that almost nobody will know or even be able to understand by looking up? Also "lens'" is incorrect; must be "lens's". Dicklyon (talk) 20:07, 6 February 2011 (UTC)
- It is simply irrelevant to this article. --Redbobblehat (talk) 22:15, 6 February 2011 (UTC)
- What is irrelevant? To say that focal length specifies the magnification of distant objects? Seems like kind of a primary thing to me. Dicklyon (talk) 22:57, 6 February 2011 (UTC)
- OK, but I don't think the word "specifies" accurately (or usefully) describes the relationship between focal length and magnification. I do think the magnification article is the best place to deal with it in sufficient detail. --Redbobblehat (talk) 14:54, 7 February 2011 (UTC)
- What is irrelevant? To say that focal length specifies the magnification of distant objects? Seems like kind of a primary thing to me. Dicklyon (talk) 22:57, 6 February 2011 (UTC)
- It is simply irrelevant to this article. --Redbobblehat (talk) 22:15, 6 February 2011 (UTC)
- The formal definition "indicates the distance between the lens' rear nodal point and focal plane" doesn't really tell you anything useful unless you already understand nodel points. The explanation in terms of magnification and equivalent pinhole, on the other hand, stands alone. Why would you want to obscure the meaning by putting it in terms of concepts that almost nobody will know or even be able to understand by looking up? Also "lens'" is incorrect; must be "lens's". Dicklyon (talk) 20:07, 6 February 2011 (UTC)
- Magnification of distance objects (at infinity, effectively) is a size-per-angle thing, quite different from the more general use of magnification that depends on object distance. It is very simply related to focal length, effectively defining focal length. Focal length is exactly magnification of distant objects, in units of mm (or other distance) per radian of object size. Dicklyon (talk) 16:26, 7 February 2011 (UTC)
focal length of a pinhole camera ?
[edit]To my understanding, a pinhole camera cannot have a "focal length" because it has no refractive or reflective optics. I can see how the pinhole kind of converges and diverges light - in that the pinhole itself is a kind of focal point, but I doubt this fits the accepted definition of focal length. Can anyone clarify ? --Redbobblehat (talk) 15:21, 7 February 2011 (UTC)
- Using a semantic argument based on the gaussian definition, you could say that the distance from nodal point to focus is zero, as is focus to toepler point - so focal length of a pinhole = 0mm ? It doesn't seem very useful though ... --Redbobblehat (talk) 15:34, 7 February 2011 (UTC)
Has somebody said that a pinhole has a focal length? It can serve as a crude imager of any focal length; that is, can have the same mm per radian magnification by placing it that many mm from an imaging plane. Dicklyon (talk) 16:22, 7 February 2011 (UTC)
- When someone says a pinhole camera has a focal length, they almost certainly are referring to the distance from the pinhole to the image plane. That is the only number that makes sense, and that lets you work out what the projection will look like with the pinhole camera model. In terms of its ability to focus light, of course, a pinhole has zero power (infinite focal length) in Gaussian optics and has effectively negative focal length if you consider diffraction. —Ben FrantzDale (talk) 14:32, 28 October 2011 (UTC)
- This is one of the reasons why I dislike the pinhole camera model—a pinhole camera is really very different from a conventional camera, and the model leads people to incorrect assumptions about how cameras work.--Srleffler (talk) 17:22, 28 October 2011 (UTC)
@Redbobblehat Assuming the pinhole is of finite size, so parallel rays can in fact go through it, the focal length is surely infinity: the rays remain parallel after passing through the pinhole, and therefore never meet. So 1/f is always zero, and only an object at infinity can be in focus. This seems accurate, since rays from the same point which graze opposite edges of the pinhole will diverge unless it's infinitely far away.
Edit: I missed one of the possibilities. With 1/f = 0, the two possibilities are
- real image, with object and image both at infinity
- virtual image (negative image distance), at the same distance as the object.
This "virtual image" is simply your view of the object in its actual location, on looking at it through the pinhole. Also I notice that the aperture of the pinhole is f/infinity, so a pinhole photo which is in focus it will also be completely dark. Which makes sense considering the film is infinitely far from the pinhole.Musiconeologist (talk) 21:04, 18 March 2024 (UTC)
Subject distance aka focal distance aka focus distance aka object distance
[edit]Many of our discussions above have touched on the common confusion of terminology that "focal length" means the distance from the subject to the entrance pupil when really that's referred to variously as "subject", "focus", and "object" distance. I can't find a subject distance page on Wikipedia, and it may not warrant its own article, but I think it needs something (perhaps on this page?). Related is that some camera lenses have a fixed focal length (such as the Cannon EF 50mm f/1.8 II), and it is focused my moving all elements together (presumably changing the angle of view as it focuses because the pinhole camera model focal length would be changing (unless it were image-space telecentric). On the other hand, there may be lenses that change their focal length (?) via internal focusing, and then there are liquid lenses that can change their focal length and so could be used to focus or (in principal) to zoom. Thoughts? —Ben FrantzDale (talk) 14:32, 28 October 2011 (UTC)
- Is this a common confusion of terminology? Focal length is not the distance from the subject to the entrance pupil. I'm not sure that the fact that it is not is worth mentioning,unless there is evidence that many people think it is.--Srleffler (talk) 17:29, 28 October 2011 (UTC)
In Photography
[edit]There should be a section with a sample of how the focal length affects the background and subject of the photograph if the photographer moves forward and backward. See this article http://photo.tutsplus.com/tutorials/photography-fundamentals/exploring-how-focal-length-affects-images/ — Preceding unsigned comment added by 74.64.108.61 (talk) 23:20, 16 January 2012 (UTC)
- See also: Dolly zoom. —Ben FrantzDale (talk) 18:29, 17 January 2012 (UTC)
Definition in lede?
[edit]The lede says, For an optical system in air, it is the distance over which initially collimated rays are brought to a focus. Do we need to specify, in air? Isn't this the same definition in a vacuum (or any other medium)? -- RoySmith (talk) 15:36, 31 May 2015 (UTC)
- If the medium has an index of refraction other than one, the point where those rays are brought to focus is not one focal length away from the lens. This is unintuitive. See Greivenkamp's book for details.--Srleffler (talk) 05:05, 1 June 2015 (UTC)
equations for General optical systems
[edit]Hello. First, let me thank you for a great page. I just saw it for the first time a few minutes ago. I have a couple of questions: There is this line: "(n is the refractive index of the substance from which the lens itself is made; n1 is the refractive index of any medium in front of the lens; n2 is that of any medium in back of it)." "n" is used in the equations, but n1 and n2 are not. ??? Then, the following equation seems to be for a simple system with two lenses, because it has R1 and R2 terms. Plus, each lens has 2 radii, so I'm confused there. == Pardon, on re-reading, that equation seems to be for one lens. So there are no equations for optical systems of 2 or more lenses? That would be much appreciated.
What are the equations for systems with 3, 4, or 5 elements? (I am an avid photographer, and some of my better lenses have 7 elements.) If I saw the general pattern for how the equation expands when more lenses are added, I think I could figure out the progression. Thanks in advance, AOrange (talk) 17:37, 18 August 2015 (UTC)
- The formula for focal length that is given is for a lens in air, that is n1 = n2 = 1. The article should perhaps be clearer about this. Yes, the equation is for a single lens with two surfaces of radii R1 and R2.
- If you want to consider systems with more than one lens, you have to take into account the spaces between them. You can derive a formula for any given system, but doing that is beyond the scope of a Wikipedia article; you really need an undergraduate course in optics.--Srleffler (talk) 02:33, 19 August 2015 (UTC)
Case of multiple lenses stacked— how does this work?
[edit]I've read over this article several times trying to get a good grasp of it. In the section where it talks about "General optics", the subject of a thick lens is brought up, and is compared to a system containing several lenses as opposed to a single thin lens. However, the equations which follow this only make reference to the refractive index of a single lens, and the other aspects (thickness, radius of curvature, etc.) of that lens. I don't understand (yet) how this then compares to a system with multiple lenses in it (with possibly multiple refractive indices, etc.). Could we get some kind of explanation of how that works? (or is that beyond the technical scope of this article, and if so, then surely it should go SOMEwhere and where else if not here?). On another point, I am finding myself disoriented at having to know the refractive index and curvature of my thick lens before I can compute its effective focal length— if I had such a lens in front of me, and didn't know for certain its refractive index or its curvature, would there be no way for me to compute its EFL? (Or could I treat it as a special case of a thin lens in air, which does not require these unusual parameters to actually compute? Note that I don't mean "unusual" as in "unknowable" I mean it in the sense of "not often being found on hand at the moment a person might want to find out the focal length of a thick lens", yes?). Please advise, one of you all who have much more experience with this than I. Thanks! KDS4444Talk 09:09, 21 September 2015 (UTC)
- Determining the focal length of a general multi-lens system is beyond the scope of an encyclopedia article. There isn't a simple formula. The similarity between a thick lens and a multi-lens system is that if you know the focal length, and you know where the principal planes are, you can calculate (to first-order approximation) the imaging properties of that lens. This is an important simplification: you don't need to worry about the detailed design of the lens; just knowing the focal length tells you a lot about how it will perform.
- Why would you expect to be able to compute the EFL without knowing the parameters for that computation? That's bizarre. Opticians use a lens clock to measure the radii of curvature of a lens, and of course they know which glass it is made of and therefore its index of refraction. One can also directly measure the focal length by imaging a distant source or by other similar means.--Srleffler (talk) 02:09, 22 September 2015 (UTC)
Convex and concave
[edit]I am reverting these edits. They confuse rather than clarify. "Convex" and "concave" do not depend on what direction you are looking at the lens from. A surface of a physical object like a lens is "convex" if it bulges outward, and "concave" if it is depressed inward. Looking at it from the left or right does not change whether the surface is convex or concave. A convex surface on a lens does not become concave if you flip the lens over. Srleffler (talk) 04:45, 21 July 2024 (UTC)
- C-Class level-4 vital articles
- Wikipedia level-4 vital articles in Physical sciences
- C-Class vital articles in Physical sciences
- C-Class physics articles
- High-importance physics articles
- C-Class physics articles of High-importance
- C-Class film articles
- C-Class filmmaking articles
- Filmmaking task force articles
- WikiProject Film articles
- C-Class Photography articles
- Mid-importance Photography articles
- WikiProject Photography articles










